
Adam Inglot
Adiunkt w Katedrze Geodezji
Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
adam.inglot@pg.edu.pl
2023-02-02, aktualizacja 2023-02-05
© ainglot.pl, 2022. Udostępnianie i wykorzystanie zgodnie z licencją Creative Commons Attribution 4.0 International license (CC BY 4.0).NumPy - macierze, wielowymiarowe tabliceNumPy to podstawowy pakiet do obliczeń na tablicach w Pythonie. Biblioteka ta dostarcza nie tylko wielowymiarowe tablice, ale również szereg procedur do szybkich operacji na tablicach: matematycznych, logicznych, manipulacji kształtami, sortowania, wybierania, transformacji Fouriera, podstawowej algebry liniowej, podstawowych operacji statystycznych, symulacji losowych i wielu innych. Co ważne, obiekty NumPy przechowują dane liczbowe jak i sekwencje znaków, jednak głównie wykorzystywany jest do prowadzenia obliczeń na liczbach.
Proponowany i najczęściej używany sposób importowania moduły NumPy to: import numpy as np.
Zacznijmy od deklarowania tablicy, listy NumPy w podstawowy sposób, używając metody array. Zadeklarujmy na początku tablicę jedno wymiarową - czyli listę ale jako obiekt NumPy.
>>> import numpy as np>>> a = np.array([1, 2, 3, 4, 5])
Zadeklarujmy teraz tablice dwuwymiarową, należy pamiętać że podane wartości muszą wypełniać całą tablicę, inaczej to ujmując musimy zadeklarować tyle zmiennych dla każdego wiersza jaką mamy liczbę kolumn:
>>> a = np.array([[1, 2], [3, 4], [5, 6]])

Tworzenie listy NumPy jako ciągu z sekwencji wartości - początek, koniec, krok. Wartość krok może być liczbą zmiennoprzecinkową.
>>> b = np.arange(10, 20)>>> print(b)[10 11 12 13 14 15 16 17 18 19 ]
Rozwiązanie z krokiem, podajmy wartość zmiennoprzecinkową 2.5
>>> b = np.arange(10, 50, 2.5)>>> print(b)[10. 12.5 15. 17.5 20. 22.5 25. 27.5 30. 32.5 35. 37.5 40. 42.5 45. 47.5]
Jak zrobić listę z numerami odwrotna, z odliczaniem? użyjmy kroku -1, z tym że początek musi być większy niż koniec:
>>> b = np.arange(10, 0, -1)>>> print(b)[10 9 8 7 6 5 4 3 2 1]
Podobnym narzędziem, do budowania listy wartości w NumPy jest metoda linspace, podajemy trzy parametry - początek, koniec, liczebność. Jak to działa, podajemy zakres wartości które są początkową i końcową wartością w nowo utworzonej liście a poprzez wskazanie ile liczb ma zawierać lista, algorytm oblicza wartości pośrednie.
>>> c = np.linspace(0, 10, 21)>>> print(a)[ 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. 8.5 9. 9.5 10.]

Deklarowanie tablic dwuwymiarowych możemy wykonać kilkoma sposobami, macierze diagonalne - eye, diag, macierze wypełnione wartościami 0 - zeros, 1 - ones
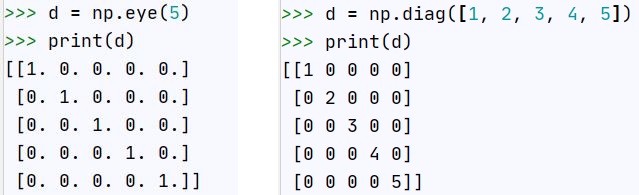
Budowanie tablicy wskazując rozmiar - liczbę wierszy i liczbę kolumn:

Przy deklarowaniu tablicy f dodatkowo wskazaliśmy typ danych - int, możemy też wskazać float. Dla tablic NumPy można wskazać precyzyjną "pojemność" liczby np. int32, int64, float32, float64. Więcej na temat typów danych można doczytać w dokumentacji NumPy.

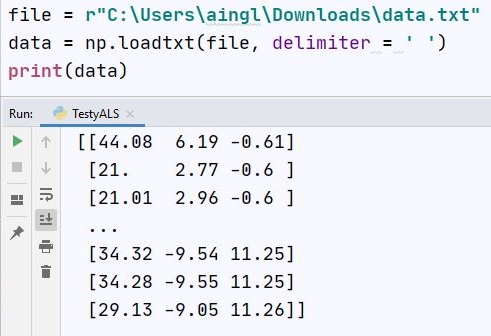
NumPyPrzykład z dokumentacji NumPy pokazuje dobrze że zmienna przechowuje odniesienie do obiektu a nie sam obiekt. Ale co to dokładnie znaczy to przestudiujmy na przykładzie:

Pierwszą linię już znamy, deklarujemy listę NumPy do zmiennej a. W drugiej linii do zmiennej b przypisujemy odniesienie do części obiektu a, dokładnie do pierwszych dwóch wartości 1, 2. Jak wydrukujemy zmienne a i b to widzimy co one zawierają. Następnie do obiektów których odniesienie mamy w zmiennej b dodajemy 1. Jak wydrukujemy ponownie obie zmienne to widzimy że zarówno w zmiennej b zwiększyliśmy wartości jak i w zmiennej a. Jeżeli nie chcemy żeby taka sytuacja miała miejsca, czyli chcemy żeby wartości w zmiennej b były niezależne od zmiennej a, zastosujemy metodę copy.

Wybranie pojedynczej wartości z tablicy odbywa się podobnie jak w przypadku list czy ciągu znaków. Selekcja pod tablicy również, podajemy zakres wartości odseparowanych dwukropkiem :.

Gdy mamy tablicę wielowymiarową to system wybierania wartości jest podobny jak w przypadku listy w liście:
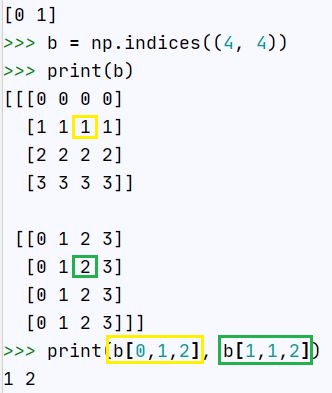
Nie podając ostatniej pozycji, z tablicy trójwymiarowej otrzymamy listę:

Budowanie listy lub tablicy na podstawie listy indeksów i tablicy z której "pobierzemy" wartości.

NumPyMając dwie tablice możemy połączyć je w jedną, pod warunkiem zgodnych rozmiaru łączenia tablic. Jeżeli łączymy tablice poszerzając je horyzontalnie (rozpatrując tablice dwuwymiarową) to musimy mieć równą liczbę wierszy, jeżeli łączymy wertykalnie, to musimy zadbać o równą liczbę kolumn.
Sprawdźmy to na przykładzie dwóch różnych tablic, zadeklarujmy tablicę A i B:


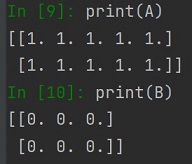
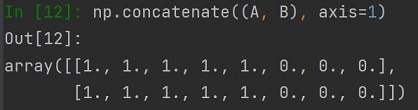
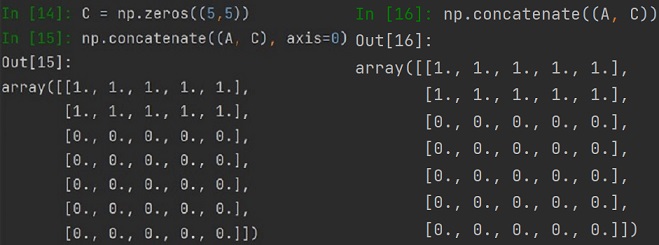
Łączenie tablic wykonujemy metodą concatenate, metoda ta przyjmuje dwie lub więcej tablic. Oprócz samych tablic do łączenia podajemy wartość wzdłuż których z "osi" (axis) będziemy łączyć tablice, domyślna wartość to 0.
NumPyWyznaczenie rozmiaru listy już pamiętamy, służy do tego metoda len(), możemy tę metodę również zastosować do obiektu array. Jednak len() podaje tylko jedną wartość rozmiaru listy czy tablicy, wartość z najwyższego wymiaru.
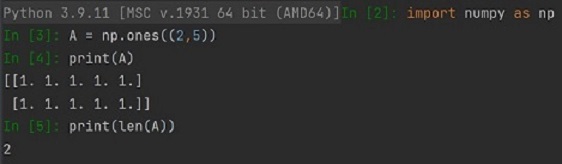
Jeżeli chcemy metodą len() sprawdzić rozmiar kolejnego wymiaru tablicy, czyli sprawdzić "liczbę kolumn", to w metodzie należy podać jedne z wierszy:
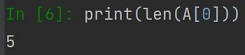
W NumPy dostępną mamy wygodniejszą metodę sprawdzania rozmiarów tablicy - shape. Metodę wywołujemy bezpośrednio na zmiennej:
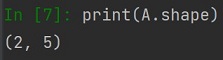
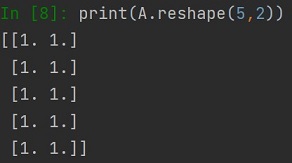
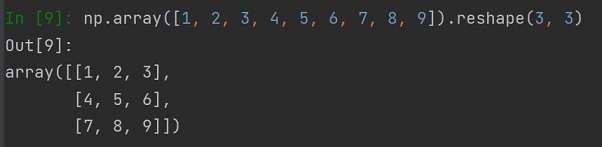
A jak zmienić rozmiar listy lub tablicy? Potrzebna nam jest metoda reshape. Przy użycia tej metody można również zmienić wymiar tablicy, np. z jednowymiarowej na dwuwymiarową.
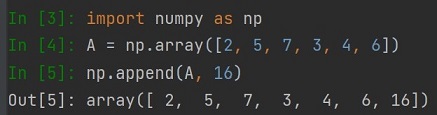
Zacznijmy od dodawania wartości do tablicy array, można to wykonać poprzez metodę append. Możemy wprowadzać pojedyncze wartości jak i całe listy:

Czy możemy dodać do listy tablicę? Tak, dlatego że metoda append przekształci nam tablicę na listę i w wyniki będziemy mieli listę:
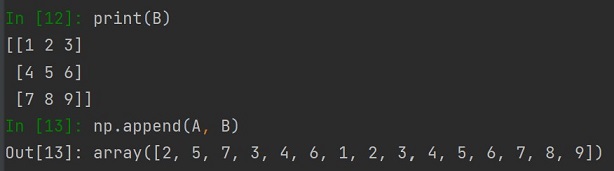
Podobnie dzieje się gdy do tablicy dodamy listę:
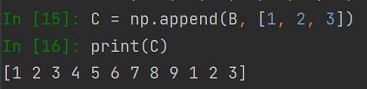
Jeżeli chcemy "wrócić" do dwuwymiarowej tablicy należy użyć metody reshape podając rozmiar tablicy:
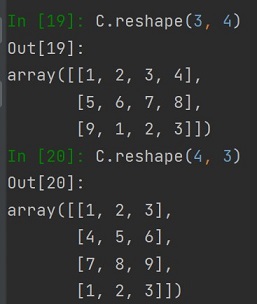
Przy obsłudze danych pojawia się potrzeba dodania, czy uzupełnienia danych w tablicy, tak też niekiedy potrzebujemy usunąć wskazany element tablicy. Wykonać można to stosując metodę delete, do tej metody podajemy tablicę oraz wskazujemy pozycję na której znajduje się element do usunięcia:

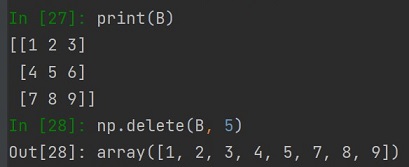
Sortowanie danych jest czynnością która wielokrotnie pomaga nam w obsłudze danych, czy analizowaniu zbioru danych. Podczas pracy na listach mięliśmy dostępną metodę sort, dla tablic NumPy mamy analogiczną metodę o tej samej nazwie np.sort.

Używając metody flip otrzymujemy listę wartości posortowanych malejąco:

SciPy - algorytmy matematyczneSciPy to zbiór algorytmów matematycznych i funkcji ułatwiających pracę, zbudowany na rozszerzeniu NumPy w języka Python. Dodaje on znaczną moc do interaktywnej sesji Pythona poprzez dostarczenie użytkownikowi wysokopoziomowych poleceń i klas do manipulacji i wizualizacji danych. Dzięki SciPy, interaktywna sesja Pythona staje się środowiskiem do przetwarzania danych i prototypowania systemów, rywalizującym z takimi systemami jak MATLAB, IDL, Octave, R-Lab i SciLab.
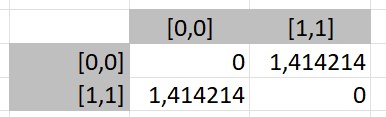
Budowanie tablicy relacji dystansu na zasadzie "każdy z każdym", dostarczamy dwie tablice dwuwymiarowe o rozmiarze (n, 2) - czyli tablicę ze współrzędnymi x i y. Otrzymujemy tablicę odległości kartezjańskiej pomiędzy parami współrzędnych.
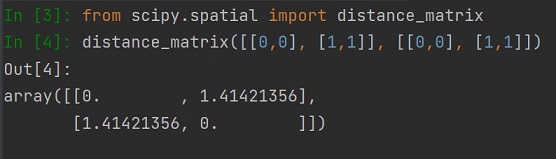
Wizualizacja obliczeń:
mathplotlib - wizualizacja danychMatplotlib to wszechstronna biblioteka do tworzenia statycznych, interaktywnych wizualizacji w Pythonie . Sama bibliotek umożliwia budowę różnych wykresów w dość tradycyjnej, może nieco mniej atrakcyjnej graficznie formie, jednak dzięki tej bibliotece możemy w dość prosty sposób przedstawić wyniki analiz zbiorów danych. Jeżeli chcemy wykonać atrakcyjny graficznie wykres najlepiej zaglądnąć do biblioteki Seaborn.
Ten rodzaj wykresu jest często stosowany do prezentacji danych, czy również do kontroli danych w przypadku dużych zbiorów - wykonując wizualizację danych łatwiej wyłapać błędy lub braki.
Przeglądnijmy najprostszy możliwy przykład:
1import matplotlib.pyplot as plt23value = [1, 2, 3, 4, 5]45fig, ax = plt.subplots()6ax.bar(value, value, .9)78plt.show()
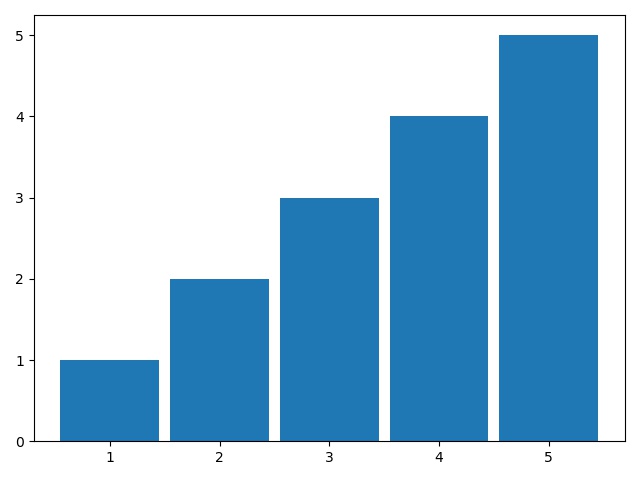
Omówmy poszczególne elementy powyższego skryptu. Linia 1 to importowanie moduły pyplot jako plt - moduł do uruchamiania oraz określenia wielkości, rozdzielczości wykresu. W 3 linii wprowadzamy listę z danymi. Następnie, w linii 5 przypisujemy do dwóch zmiennych argumenty jakie zwraca funkcja plt,subplots(), pierwszy argument to jest rysunek (figure), drugi argument to wykres (axes), jeden rysunek może zawierać kilka wykresów. Kolejna linia 6, określamy rodzaj wykresu oraz wskazujemy dane i podajemy parametry, na pierwszej pozycji value podaliśmy dane na podstawie których będą budowane słupki, na drugiej pozycji, również lista value, jednak w tym przypadku jako etykiety i pozycja danych na osi y, ostatni argument trzeci - wartość 0.9 - to szerokość kolumny. Ostatnia 8 linia wywołuje funkcję prezentującą zbudowany wykres jako osobne okno.
1import matplotlib.pyplot as plt23value = [1, 2, 3, 4, 5]4labels = ['A', 'B', 'C', 'D', 'E']56fig, ax = plt.subplots()7ax.bar(value, value, .9)89ax.set_xticks(value, labels)1011plt.show()
UWAGA - może wystąpić konieczność aktualizacji biblioteki matplotlib, aktualna wersja ArcGIS, a za tym idzie środowisko anakondy (Python + biblioteki) zainstalowane wraz z wrsją ArcGIS Pro 3.0.3 to wersja 3.4.3. Konieczna jest wersja co najmniej 3.5.0. Aktualizację można wykonać na trzy sposoby, przez PyCharm, ArcGIS Pro lub przez wiersz poleceń.
PyCharm:
W menu głównym PyCharm, przejdź do File, następnie Settings...:
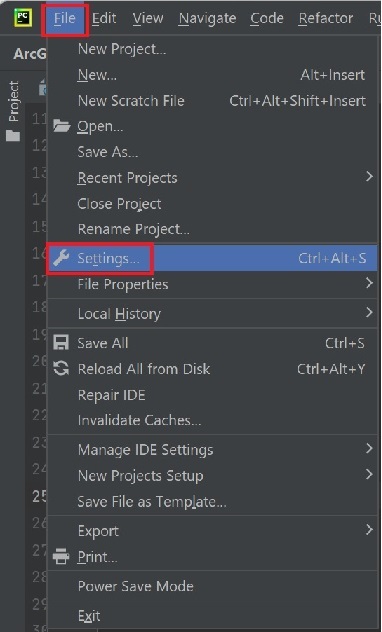
W ustawieniach (Settings) rozwiń Project:ArcGISPro i wskaż Python Interpreter:
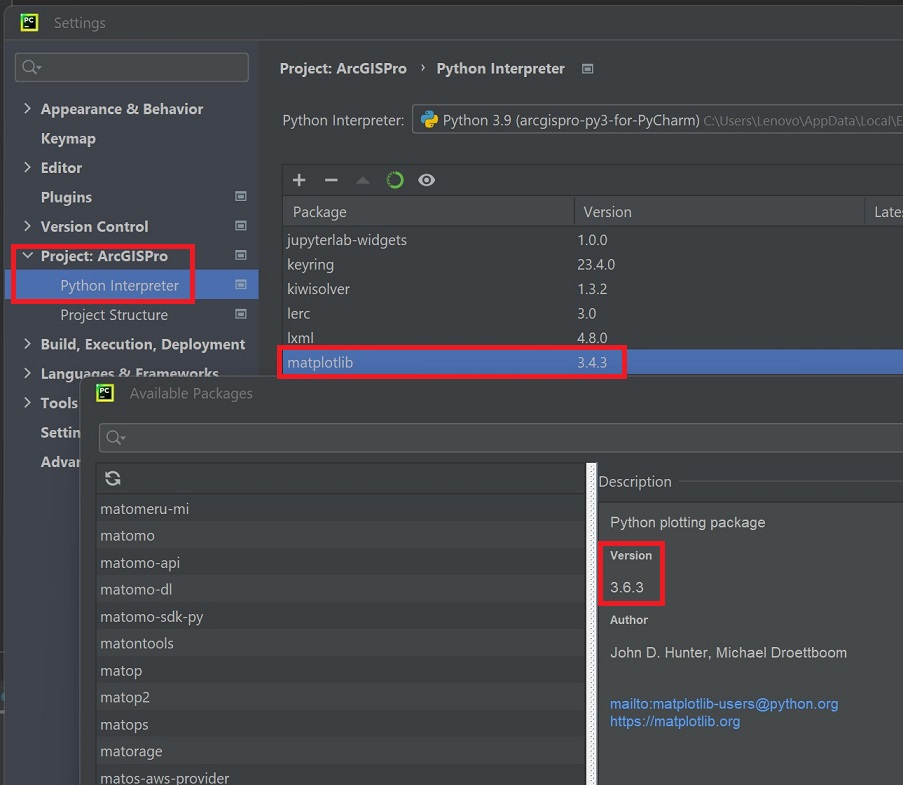
ArcGIS Pro:
Po uruchomieniu ArcGIS Pro, nie otwieraj projektu tylko przejdź do Settings - po lewej stronie okna.
Następnie wskaż
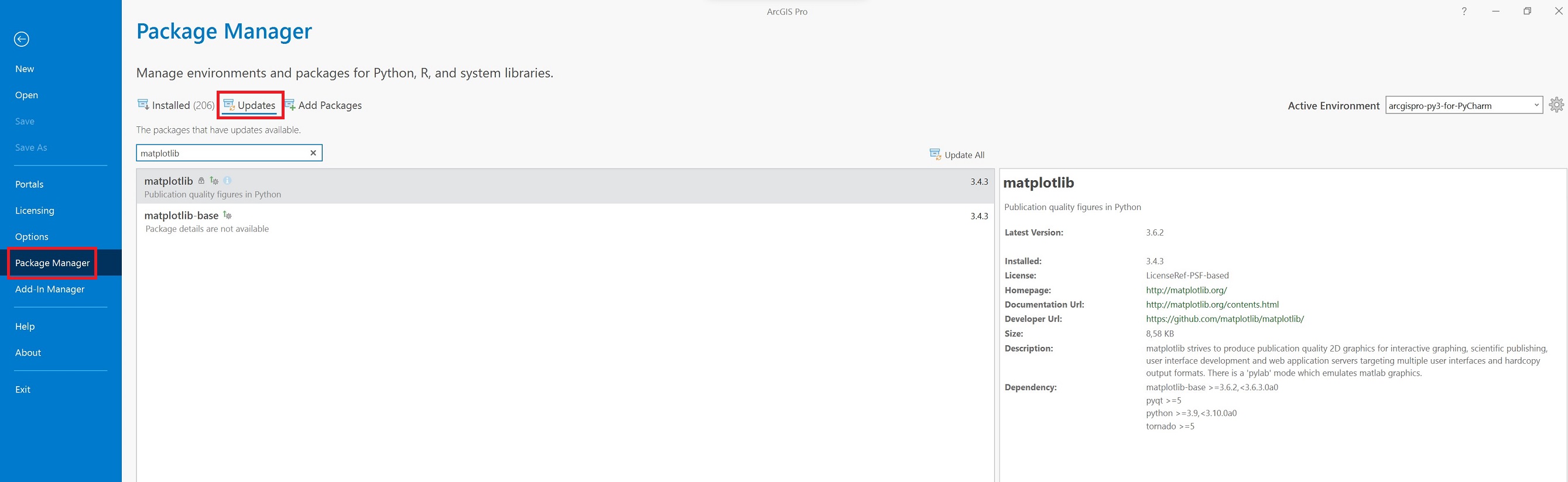
Wiersz poleceń Windows:
Po uruchomieniu wiersza poleceń wpisz polecenie pip install matplotlib==3.6.3
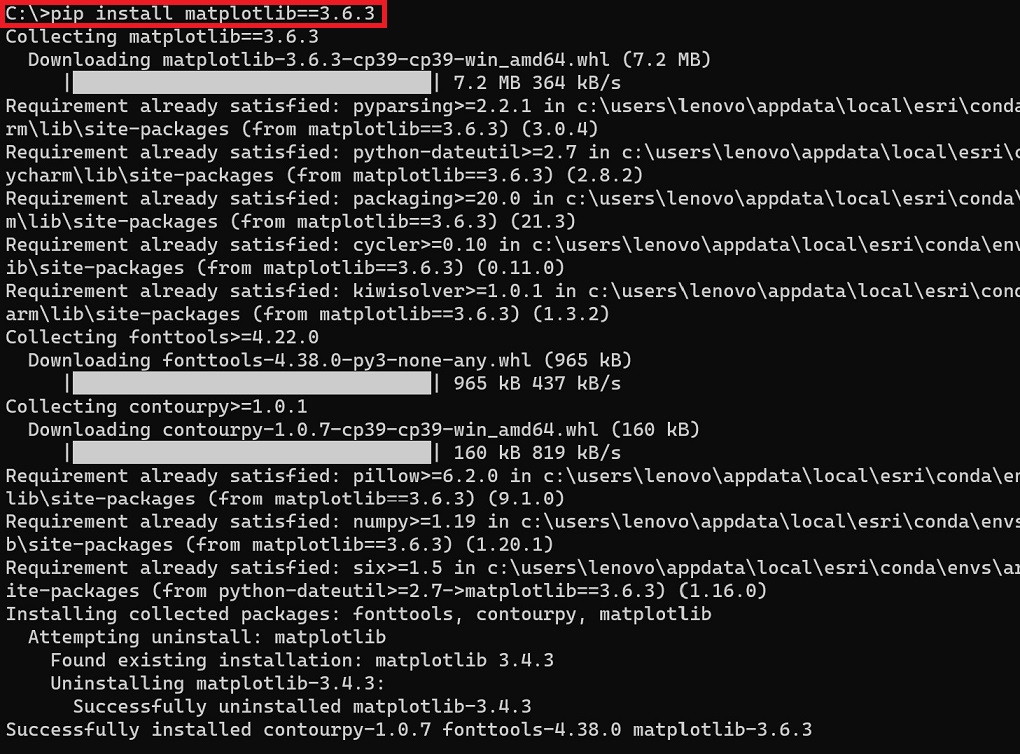
W przypadku gdy chciałem wykonać aktualizacji biblioteki, udało mi się to wykonać dopiero poprzez wiersz poleceń.
Wykonując skrypt otrzymamy poniższy wykres:
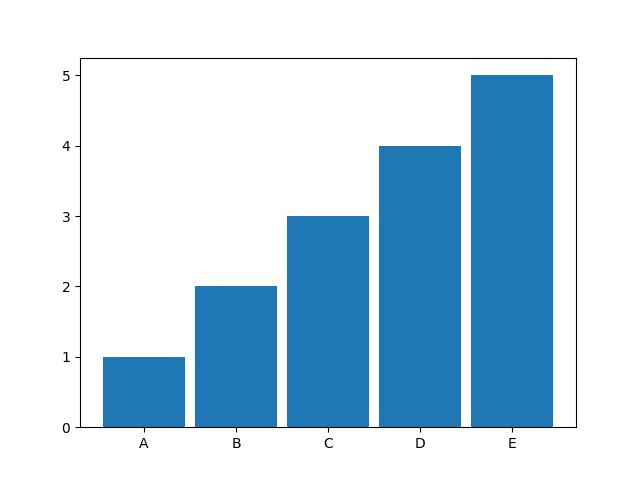
W skrypcie dodaliśmy listę z etykietami - labels (linia 4), oraz użyliśmy metody set_xticks (linia 9) przyjmującej dwa argumenty, pierwszy to wskazanie pozycji na osi x a drugi to wskazane etykiety odpowiednio uszeregowane.
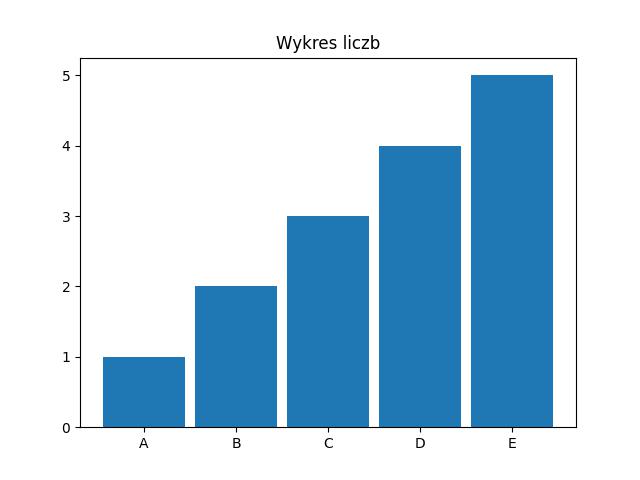
Tytuł wykresu wstawiamy metodą set_title() która przyjmuje jeden argument w formie cięgu znaków - string.
1import matplotlib.pyplot as plt23value = [1, 2, 3, 4, 5]4labels = ['A', 'B', 'C', 'D', 'E']56fig, ax = plt.subplots()7ax.bar(value, value, .9)89ax.set_xticks(value, labels)10ax.set_ylabel('Liczby')11ax.set_title('Wykres liczb')1213plt.show()
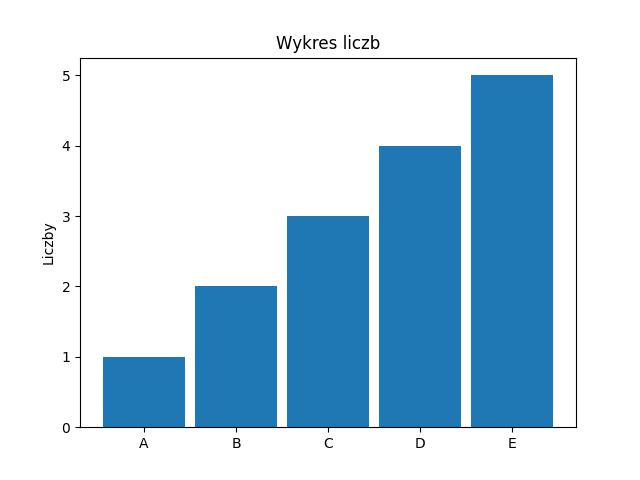
Dodajmy jeszcze opis osi wykresu dla osi y.
1import matplotlib.pyplot as plt23value = [1, 2, 3, 4, 5]4labels = ['A', 'B', 'C', 'D', 'E']56fig, ax = plt.subplots()7ax.bar(value, value, .9)89ax.set_xticks(value, labels)10ax.set_ylabel('Liczby')11ax.set_title('Wykres liczb')1213plt.show()
Najlepszym sposobem na dopasowanie wykresu do danych które chcemy zaprezentować jest przegląd galerii wykresów na stronach matplotlib-gallery.
Wykresy punktowe naturalnie mogą nam się przydać do szybkiego i prostego wyświetlenia współrzędnych punktowych w oknie matplotlib.
1import matplotlib.pyplot as plt2import random34x = random.sample(range(50,100), k=30)5y = random.sample(range(50,100), k=30)6r = [random.randint(50,100) for i in range(30)]78fig, ax = plt.subplots()9ax.scatter(x, y, s=r, marker='o')1011plt.show()
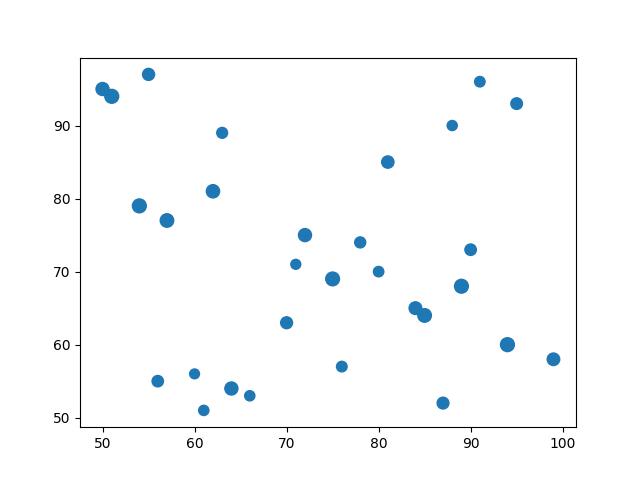
Pewnie już zauważyliśmy że osie wykresów dopasowują się do zakresu wartości danych. Spróbujmy ustawić zakres osi x i y niezależnie od zakresu współrzędnych.
1import matplotlib.pyplot as plt2import random34x = random.sample(range(50,100), k=30)5y = random.sample(range(50,100), k=30)6r = [random.randint(50,100) for i in range(30)]78fig, ax = plt.subplots()9ax.scatter(x, y, s=r, marker='o')1011plt.ylim([25, 125])12plt.xlim([25, 125])1314plt.show()
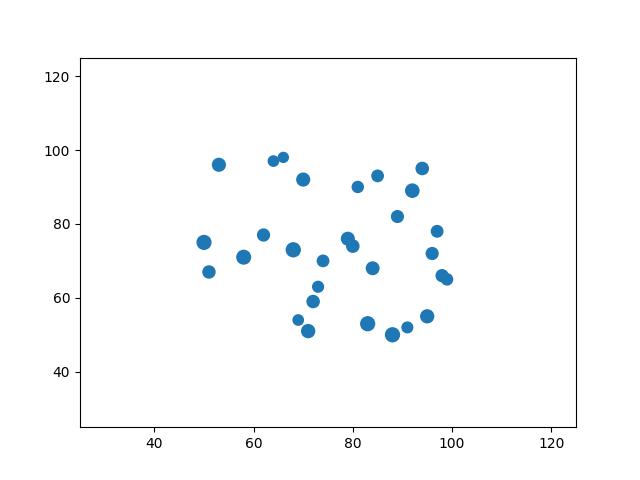
Dodaliśmy limit, zakres wartości odnoszące się do osi x i y. Wstawione limit mogą powodować umieszczenie danych poza obszarem wykresu. Oczywiście, w przykładzie powyżej jest to nie możliwe, ze względu na to że podany limit osi jest większy niż przedział losowanych liczb dla współrzędnych x i y.
[1] Informatyka - materiały do nauki. http://informatyka2.orawskie.pl/, (data dostępu 28.09.2022).
[2] Mark Summerfield, Python 3 - kompletne wprowadzenie do programowania. Helion, wydanie 2, ISBN: 978-83-246-2642-7, 2010.